Самостоятельная работа 15: стандартные алгоритмы II

Цели: изучение элементов алгоритмизации и обобщённого программирования на основе библиотеки стандартных алгоритмов C++.

Определения и примеры

Пример 1

Группа примеров на основе пользовательского класса итератора.

Int_iterator

Определим итератор, позволяющий проходить по последовательности целых чисел. Тип целых будем передавать через параметр шаблона Int.

/// Итератор, реализующий представление промежутков ряда целых чисел.
template <class Int = int>
class Int_iterator
{
  Int val;

public:
  using value_type = Int;
  using reference = const value_type&;
  using pointer = const value_type*;
  using difference_type = Int;
  using iterator_category = std::random_access_iterator_tag;

Для того, чтобы итератор можно было использовать вместе со стандартными алгоритмами, требуется, чтобы был определён ряд вспомогательных типов. Класс итератора может определить их как вложенные объявления типов:

Если в качестве итератора требуется использовать некий тип, который определяем не мы, и который не содержит указанных объявлений типов, но может быть использован в качестве итератора, то набор указанных типов может быть заявлен через частную специализацию стандартного класса iterator_traits. Например, в случае Int_iterator<T> она могла бы выглядеть так (все те же объявления вложенных типов):

namespace std {
template <class Int>
struct iterator_traits<Int_iterator<Int>>
{
  using value_type = Int;
  using reference = const value_type&;
  using pointer = const value_type*;
  using difference_type = Int;
  using iterator_category = std::random_access_iterator_tag;  
};}

Продолжим рассмотрение определения класса Int_iterator.

Определим конструктор, создающий итератор, начинающий отсчёт с числа val. Определим также элементарные операторы разыменования (* и ->), а также инкремента и декремента.

  explicit Int_iterator(Int val = 0)
    : val(val) {}

  reference operator*() const { return val; }
  pointer operator->() const { return &val; }

  Int_iterator& operator++()
  {
    ++val;
    return *this;
  }
  
  Int_iterator& operator--()
  {
    --val;
    return *this;
  }

Данные определения инкремента и декремента определяют только префиксные варианты данных операций. Для определения постфиксных вариантов в стандарте языка закреплена форма с фиктивным параметром типа int:

  Int_iterator operator++(int)
  {
    auto old = *this;
    ++(*this);
    return old;
  }

  Int_iterator operator--(int)
  {
    auto old = *this;
    --(*this);
    return old;
  }

Так как наш итератор является итератором произвольного доступа, следует определить все вариации +, -, +=, -=. Они действуют аналогично соответствующим операциям на указателях (итераторы имитируют указатели).

  Int_iterator& operator+=(difference_type delta)
  {
    val += delta;
    return *this;
  }

  Int_iterator& operator-=(difference_type delta)
  {
    val -= delta;
    return *this;
  }

  Int_iterator operator-(difference_type delta) const
  {
    return Int_iterator<Int>(val - delta);
  }

  difference_type operator-(Int_iterator rhs) const
  {
    return val - rhs.val;
  }
};

Операцию + и операции сравнения (шесть штук), определим как функции, внешние к классу.

template <class Int>
bool operator==(Int_iterator<Int> a, Int_iterator<Int> b)
{
  return *a == *b;
}

template <class Int>
bool operator!=(Int_iterator<Int> a, Int_iterator<Int> b)
{
  return *a != *b;
}

template <class Int>
bool operator<(Int_iterator<Int> a, Int_iterator<Int> b)
{
  return *a < *b;
}

template <class Int>
bool operator<=(Int_iterator<Int> a, Int_iterator<Int> b)
{
  return *a <= *b;
}

template <class Int>
bool operator>(Int_iterator<Int> a, Int_iterator<Int> b)
{
  return *a > *b;
}

template <class Int>
bool operator>=(Int_iterator<Int> a, Int_iterator<Int> b)
{
  return *a >= *b;
}

template <class Int>
Int_iterator<Int> operator+(Int_iterator<Int> a, Int delta)
{
  return a += delta;
}

template <class Int>
Int_iterator<Int> operator+(Int delta, Int_iterator<Int> a)
{
  return a + delta;
}

Для удобства создания объектов класса Int_iterator определим функцию-шаблон int_iterator. Таким образом, тип Int (параметр шаблона Int_iterator) будет выводиться автоматически по типу переданного параметра, и его не надо будет указывать явно (если требуется указать явно, то следует вызвать конструктор Int_iterator непосредственно).

template <class Int>
Int_iterator<Int> int_iterator(Int n)
{
  return Int_iterator<Int>(n);
}

Простые примеры

Запись последовательности чисел n, n+1, n+2, …, m в последовательность по итератору out с помощью Int_iterator можно выполнить стандартным алгоритмом copy:

copy(int_iterator(n), int_iterator(m + 1), out);

Например, вывести в стандартный поток вывода можно так (заменим out на итератор вывода в ostream, который будет выводить в поток cout и после каждого вывода в качестве разделителя выводить строку "\t", т. е. символ табуляции):

copy(int_iterator(n), int_iterator(m + 1), 
       ostream_iterator<int>(cout, "\t"));

Данный код несложно обернуть в функцию-шаблон, действующую наподобие стандартных алгоритмов (напоминающую, кстати, стандартную функцию iota):

template <class Int, class OutIt>
OutIt count_up(Int n, Int m, OutIt out)
{
  return std::copy(
    int_iterator(n), int_iterator(m + 1), out);
}

Далее примеры будут подаваться именно в виде таких обобщённых функций. Например, с помощью transform, принимающей две последовательности и бинарную операцию, легко реализовать вывод последовательности квадратов целых чисел:

/// Вывод последовательности квадратов натуральных чисел от 1 до n
/// в последовательность по итератору out.
template <class Int, class OutIt>
OutIt squares(Int n, OutIt out)
{
  return std::transform(
    int_iterator(1), int_iterator(n + 1),
    int_iterator(1),
    out, std::multiplies<Int>());
}

Теперь вывести последовательность квадратов в стандартный поток вывода можно, например, так:

squares(n, ostream_iterator<int>(cout, "\n"));

Стандартный класс ostream_iterator является шаблоном по типу выводимых значений. Это приводит к необходимости указывать этот тип явно (выше был int). Можно ли написать аналог ostream_iterator, который будет выводить значения произвольного типа?

С помощью комбинации Int_iterator и стандартной функции inner_product легко записать вычисление суммы квадратов натуральных чисел:

/// Сумма квадратов натуральных чисел от 1 до n.
template <class Int>
Int squares_sum(Int n)
{
  const Int zero = 0, one = 1, end = n + 1;
  return std::inner_product(
    int_iterator(one), int_iterator(end),
    int_iterator(one), zero);
}

Конечно, подобное действие ещё легче сделать обычным циклом. Но простота данного примера обманчива: очень похожие конструкции, учитывая обобщённый (“шаблонный”) характер совмещаемых в них компонентов, могут обладать действительно сложным поведением, однако при должном навыке и опыте такой код довольно легко читать.

С помощью стандартной функции partial_sum и стандартного функтора multiplies можно эффективно реализовать вывод последовательности факториалов. Каждое следующее число получается одним домножением:

/// Вывод 1!, 2!, ..., n! в последовательность по итератору out.
template <class Int, class OutIt>
OutIt factorials(Int n, OutIt out)
{
  return std::partial_sum(
    int_iterator(1), int_iterator(n + 1),
    out, std::multiplies<Int>());
}

Таблица умножения

Определим функцию, выводящую фактически арифметическую последовательность с шагом a. Можно было бы модифицировать класс Int_iterator, сделав параметром также шаг приращения (в оригинальном варианте — единица). Впрочем, здесь для достижения той же цели использована комбинация transform и стандартного конструктора функторов bind, позволяющего из произвольного функтора создать новый функтор, зафиксировав значения некоторых из его параметров. В нашем случае мы бинарный функтор multiplies (выполняющий умножение) превращаем в унарный функтор, зафиксировав в качестве значения первого параметра a — получается функтор, выполняющий умножение своего параметра на число a.

/// Записать произведения a*1, a*2, ..., a*n в последовательность по итератору out.
template <class Int, class OutIt>
OutIt mult_seq(Int a, Int n, OutIt out)
{
  return std::transform(
    int_iterator(1), int_iterator(n + 1),
    out, std::bind(std::multiplies<Int>(), a, std::placeholders::_1));
}

В свою очередь, a может проходить ряд целых чисел, что позволит заполнить матрицу размера n × n таблицей умножения натуральных чисел. Параметр out задаёт последовательность контейнеров, в которые будут добавлены элементы, составляющие строки таблицы:

/// Применить mult_seq для a=1, ..., n, записывая результаты 
/// в последовательность контейнеров по итератору out.
template <class Int, class OutIt>
OutIt mult_table(Int n, OutIt out)
{
  std::for_each(
    int_iterator(1), int_iterator(n + 1),
    [n, &out](Int a)
    {
      mult_seq(a, n, std::back_inserter(*out++));
    });
  return out;
}

// от 1 до 9:
vector<vector<int>> table(9);
mult_table(9, begin(table));

ostream_iterator<int> c_out(cout, "\t");
for (auto &row : table)
{
  copy(begin(row), end(row), c_out);
  cout << '\n';
}

Последовательность простых чисел

Рассмотрим задачу генерации последовательности простых чисел.

Определим функтор, проверяющий, делится ли некоторое число, заданное в момент создания объекта функтора (и сохранённое в поле m), на переданное ему число (аргумент n оператора ()).

/// Проверить, делится ли m на n.
template <class Int>
class Is_divisible
{
  Int m;

public:
  explicit Is_divisible(Int m)
    : m(m) {}

  bool operator()(Int n) const
  {
    return m % n == 0;
  }
};

template <class Int>
Is_divisible<Int> is_divisible(Int m)
{
  return Is_divisible<Int>(m);
}

Функция is_divisible создаёт объект функтора, автоматически выводя тип параметра шаблона.

Всю приведённую выше конструкцию можно записать намного короче, если компилятор в должной мере поддерживает стандарт C++14. Для этого воспользуемся замыканием:

/// Вместо закомментированного кода, вариант C++14:
template <class Int>
auto is_divisible(Int m)
{
  return [m](Int n) { return m % n == 0; };
}

Вызов is_divisible создаёт функтор, далее (2) уже вызывает новосозданный функтор для параметра n = 2:

assert(is_divisible(10)(2)); // 10 делится на 2

С помощью функции is_divisible легко написать функцию, получающую (перебором) последовательность всех делителей заданного числа.

/// Вывести только те числа из 2, ..., n, на которые делится m.
template <class Int, class OutIt>
OutIt divisors(Int n, Int m, OutIt out)
{
  return std::copy_if(
    int_iterator(2), int_iterator(n + 1),
    out, is_divisible(m));
}

Аналогично, можно проверить, удовлетворяет ли какое-либо число из диапазона предикату “являться делителем”. Здесь удобно применить стандартную функцию none_of. Саму проверку обернём в структуру, которую, в свою очередь, будет удобно использовать в качестве предиката. Сразу создадим объект данной структуры is_prime, который можно использовать как функтор и без необходимости указывать тип чисел явно.

/// Проверить (перебором делителей) простоту числа n.
const struct Is_prime
{
  template <class Int>
  bool operator()(Int n) const
  {
    return std::none_of( // эффективнее перебирать до кв.корня + 1
      int_iterator(2), int_iterator(n / 2 + 1),
      is_divisible(n));
  }
} is_prime;

Теперь достаточно применить предикат is_prime в качестве фильтра (через алгоритм copy_if) к последовательности чисел, чтобы записать в последовательность, заданную итератором вывода out, только простые числа из некоторого диапазона натуральных чисел:

/// Вывести простые числа из диапазона 2, ..., n.
template <class Int, class OutIt>
OutIt primes(Int n, OutIt out)
{
  return std::copy_if(
    int_iterator(2), int_iterator(n + 1),
    out, is_prime);
}

Пример 2

Рассмотрим пример 2 из работы 8. Тот пример не использовал средств обобщённого программирования и стандартных алгоритмов C++. “Модернизируем” его, сделав классы вектора и точки шаблонами и все алгоритмы — шаблонами, позволяющими использовать разные способы хранения точек.

Заголовочный файл ageo2d.hpp “переведён” практически механически.

Теперь разберёмся с реализацией алгоритма выпуклой оболочки и тестами, заменяя подходящие циклы на вызовы стандартных алгоритмов.

Итак, будем просматривать текст jarvis.cpp сверху вниз. Первый вариант каждой функции — шаблон на основе исходного кода из примера к работе 8, второй вариант — он же, но уже использующий стандартные алгоритмы.

find_highest_rightmost

/// В диапазоне точек найти самую верхнюю из самых правых.
template <class P2_FwdIt>
P2_FwdIt find_highest_rightmost(P2_FwdIt begin, P2_FwdIt end)
{
  if (begin == end)
    return end;

  auto x_max = begin->x, y_max = begin->y;
  auto cur_max = begin;
  while (++begin != end)
  {
    if (x_max < begin->x
     || begin->x == x_max && y_max < begin->y)
    {
      x_max = begin->x;
      y_max = begin->y;
      cur_max = begin;
    }
  }

  return cur_max;
}

Имеем поиск максимума на основе лексикографического сравнения x и y координат. Обобщённый компаратор лексикографического сравнения по x, y может быть записан так:

/// Сравнение по x, затем по y (лексикографическое сравнение векторов и точек).
const struct Less_xy
{
  template <class P1, class P2>
  bool operator()(const P1 &a, const P2 &b) const
  {
    return a.x < b.x || a.x == b.x && a.y < b.y;
  }
} less_xy;

Теперь find_highest_rightmost может быть реализована как вызов std::max_element:

template <class P2_FwdIt> inline
P2_FwdIt find_highest_rightmost(P2_FwdIt begin, P2_FwdIt end)
{
  return std::max_element(begin, end, less_xy);
}

max_cw_turn

/// В диапазоне точек найти самый дальний поворот по часовой стрелке от точки v.
template <class P2_FwdIt, class P2>
P2_FwdIt max_cw_turn(P2_FwdIt begin, P2_FwdIt end, const P2 &v)
{
  if (begin == end)
    return end;

  auto cur_max = begin;
  auto vector = *begin - v; // воспользуемся оператором минус, определённым для точек выше
  while (++begin != end)
  {
    const auto new_vector = *begin - v;
    const auto cp = crossp(vector, new_vector);
    if (cp < 0.   // поворот от vector к new_vector по ЧС?
     || cp == 0.  // коллинеарны, но сонаправленны и new_vector длиннее, чем vector?
     && dotp(vector, vector) < dotp(vector, new_vector))
    {
      cur_max = begin;
      vector = new_vector;
    }
  }

  return cur_max;
}

Нетрудно видеть, что это тоже своего рода поиск максимума. Извлечём компаратор по углу/длине радиуса-вектора:

/// Сравнение радиусов-векторов точек по углу относительно заданного начала координат (origin),
/// затем по длине, если вектора коллинеарны.
template <class P>
class Less_angle
{
  P origin;

public:
  Less_angle() = default;

  explicit Less_angle(const P &origin)
    : origin(origin) {}

  bool operator()(const P &a, const P &b) const
  {
    const auto
      oa = a - origin,
      ob = b - origin;
    const auto
      cp = crossp(oa, ob);
    return cp < 0 || cp == 0 && dotp(oa, oa) < dotp(oa, ob);
  }
};

template <class P> inline
Less_angle<P> make_less_angle(const P &origin)
{
  return Less_angle<P>(origin);
}

Теперь функция max_cw_turn тоже превращается в простой вызов std::max_element.

/// В диапазоне точек найти самый дальний поворот по часовой стрелке от точки v.
template <class P2_FwdIt, class P2>
P2_FwdIt max_cw_turn(P2_FwdIt begin, P2_FwdIt end, const P2 &v)
{
  return std::max_element(begin, end, make_less_angle(v));
}

Впрочем, у данного варианта есть один недостаток по сравнению с тем, что было раньше: повторно вычисляются вектора oa = a - origin при каждом сравнении. Старый вариант запоминал последний полученный вектор.

convex_hull_jarvis

/// Алгоритм заворачивания подарка.
/// Переставляет элементы исходного диапазона точек так,
/// чтобы вершины выпуклой оболочки в порядке обхода против часовой стрелки
/// встали в начале диапазона, возвращает указатель на следущую за последней
/// вершиной построенной выпуклой оболочки вершину.
template <class P2_BidIt>
P2_BidIt convex_hull_jarvis(P2_BidIt begin, P2_BidIt end)
{
  using std::swap;
  using std::prev;
  if (begin == end)
    return end;

  // Найти позицию самой верхней из самых правых точек.
  // Это -- последняя вершина выпуклой оболочки.
  auto cur = find_highest_rightmost(begin, end);
  
  // Поставить её в конец последовательности для того,
  // чтобы корректно выйти из цикла, когда следующая вершина совпадёт с ней.
  const auto last_pos = prev(end);
  swap(*cur, *last_pos);
  cur = last_pos;

  // Цикл по вершинам выпуклой оболочки.
  while (true)
  {
    const auto next = max_cw_turn(begin, end, *cur);
    // Поставить следующую вершину.
    swap(*begin, *next);
    cur = begin++;

    if (next == last_pos) // Выпуклая оболочка построена.
      return begin;
  }
}

Несмотря на простоту цикла while в приведённом выше коде, его не так-то просто заменить на какой-либо из стандартных алгоритмов. В принципе, в такой ситуации вполне можно оставить то, что есть. Разумно использовать стандартные алгоритмы там, где они действительно хорошо подходят, а не изощряться в попытке подогнать любой код под стандартный алгоритм. Здесь как раз такой случай.

is_strictly_convex

/// Проверка многоугольника на строгую выпуклость.
template <class P2_BidIt>
bool is_strictly_convex(P2_BidIt begin, P2_BidIt end)
{
  using std::next;
  using std::prev;

  if (begin == end)
    return true; // пустое множество

  const auto begin_1 = next(begin);
  if (begin_1 == end)
    return true; // одна точка

  const auto begin_2 = next(begin_1);
  if (begin_2 == end)
    return *begin != *begin_1; // невырожденный отрезок?

  // Проходя по всем углам (парам смежных рёбер) многоугольника,
  // проверять, что поворот происходит строго против ЧС.
  auto a = *prev(end, 2), b = *prev(end);
  do
  {
    const auto c = *begin++;
    const auto // рёбра
      ba = b - a,
      cb = c - b;

    // Проверить поворот от ba к cb.
    if (crossp(ba, cb) <= 0)
      return false;

    a = b;
    b = c;
  } while (begin != end);

  return true;
}

Фактически, это линейный поиск развёрнутого угла при вершине. К сожалению, угол задаётся ровно тремя вершинами, т. е. необходимо “видеть” два элемента перед текущим, а не один, что вроде бы не даёт использовать напрямую простые алгоритмы вроде std::adjacent_find. Разумным ходом является введение итератора-адаптера, позволяющего проходить по векторам, задающим рёбра ломаной, проходя на деле по вершинам ломаной и вычисляя каждый раз разность.

Это типичный итератор ввода, так как значение, на которое он указывает, вычисляется, а не хранится в некотором контейнере.

/// Вспомогательное значение для корректной инициализации конечного итератора рёбер.
const struct End_iterator_tag {} end_iterator_tag;

/// Итератор, позволяющий перебрать отрезки (как вектора) ломаной,
/// в действительности проходя по вершинам.
template <class P_FwdIt>
class Edge_iterator
{
  P_FwdIt a, b;

public:
  Edge_iterator() = default;

  explicit Edge_iterator(P_FwdIt a)
    : a(a), b(std::next(a)) { init_val(); }

  Edge_iterator(P_FwdIt a, P_FwdIt b)
    : a(a), b(b) { init_val(); }

  Edge_iterator(P_FwdIt end, End_iterator_tag)
    : a(end) {}

  using iterator_category = std::forward_iterator_tag;
  using value_type = Vector_2<
    typename std::iterator_traits<P_FwdIt>::value_type::Coordinate>;

  using reference = const value_type&;
  using pointer = const value_type*;
  using difference_type = std::ptrdiff_t;

  Edge_iterator& operator++()
  {
    a = b;
    ++b;
    init_val();
    return *this;
  }

  Edge_iterator operator++(int)
  {
    auto old = *this;
    ++(*this);
    return old;
  }

  reference operator*() const { return val; }
  pointer operator->() const { return &val; }

  bool operator==(const Edge_iterator &other) const
  {
    return a == other.a;
  }

  bool operator!=(const Edge_iterator &other) const
  {
    return !(*this == other);
  }


private:
  value_type val;
  void init_val()
  {
    val = *b - *a;
  }
};

template <class P_FwdIt> inline
Edge_iterator<P_FwdIt> make_edge_iterator(P_FwdIt a)
{
  return Edge_iterator<P_FwdIt>(a);
}

template <class P_FwdIt> inline
Edge_iterator<P_FwdIt> make_edge_iterator(P_FwdIt a, P_FwdIt b)
{
  return Edge_iterator<P_FwdIt>(a, b);
}

template <class P_FwdIt> inline
Edge_iterator<P_FwdIt> make_edge_iterator_end(P_FwdIt end)
{
  return Edge_iterator<P_FwdIt>(end, end_iterator_tag);
}

Сравнивать рёбра будем по признаку знака угла: поворот налево (против ЧС) — положительный, поворот направо (по ЧС) — отрицательный. Реализуем компаратор с проверкой наличия поворота налево и его отрицание.

/// Компаратор "поворот направо" (против ЧС == counterclockwise == ccw).
const struct Is_ccw
{
  template <class V1, class V2>
  bool operator()(const V1 &a, const V2 &b) const
  {
    return crossp(a, b) > 0;
  }
} is_ccw;

/// Логическое отрицание is_ccw.
const struct Is_not_ccw
{
  template <class V1, class V2>
  bool operator()(const V1 &a, const V2 &b) const
  {
    return crossp(a, b) <= 0;
  }
} is_not_ccw;

Теперь запишем новый вариант нашей функции is_strictly_convex.

/// Проверка многоугольника на строгую выпуклость.
template <class P2_BidIt>
bool is_strictly_convex(P2_BidIt begin, P2_BidIt end)
{
  using std::next;
  using std::prev;

  if (begin == end)
    return true; // пустое множество

  const auto begin_1 = next(begin);
  if (begin_1 == end)
    return true; // одна точка

  const auto begin_2 = next(begin_1);
  if (begin_2 == end)
    return *begin != *begin_1; // невырожденный отрезок?

  // Проходя по всем углам (парам смежных рёбер) многоугольника,
  // проверять, что поворот происходит строго против ЧС.
  const auto end_1 = prev(end), end_2 = prev(end_1);
  const auto
    edge_begin = make_edge_iterator(begin),
    edge_end = make_edge_iterator_end(end_1);

  return is_ccw(*end_1 - *end_2, *begin - *end_1)
    && std::adjacent_find(edge_begin, edge_end, is_not_ccw)
       == edge_end;
}

Можно заметить, что суммарное количество строк не уменьшилось, а наоборот, увеличилось. Однако увеличилось оно засчёт того, что определённая часть кода была оформлена в виде отдельных компонент (компараторы и итератор рёбер), что позволяет их использовать повторно. В то же время, отдельные функции стали меньше.

Варианты

Дана последовательность контейнеров, заданная двунаправленными итераторами. Каждый контейнер в последовательности также предоставляет двунаправленный итератор.

Написать функцию-шаблон, проверяющую, что переданная последовательность является палиндромом и каждый контейнер в ней является палиндромом. Решение не должно содержать явных циклов.

Пример матрицы-палиндрома (частный случай последовательности контейнеров: матрица как последовательность строк или столбцов):

Дана последовательность строк матрицы, заданная парой итераторов. Каждая строка матрицы является контейнером.

Написать функцию-шаблон, выполняющую на переданной последовательности циклический сдвиг строк и столбцов на одно и то же число позиций (параметр функции). Решение не должно содержать явных циклов.

Выполним горизонтальный и вертикальный сдвиг на 3 позиции. Получим матрицу:

Пусть задана таблица-перестановка (отображение ℕ → ℕ). Данная таблица может быть реализована, например, через std::vector<size_t>, но решение должно принимать произвольный совместимый тип (достаточно оператора []).

Пусть дана матрица. Требуется получить новую матрицу, применив перестановку, переданную параметром, к строкам и столбцам матрицы. Решение не должно содержать явных циклов.

Дана последовательность точек на плоскости. Отсортировать точки лексикографически по x-y, удалить дубликаты и разделить полученные точки на две части (на месте) по признаку “выше”/“не выше” прямой, соединяющей самую первую точку (самую левую-нижнюю) с самой правой (самой правой-верхней).

Функция должна возвращать пару итераторов: начало и конец второй части (начало первой части совпадает с началом исходной последовательности, конец — с началом второй части). Решение не должно содержать явных циклов.

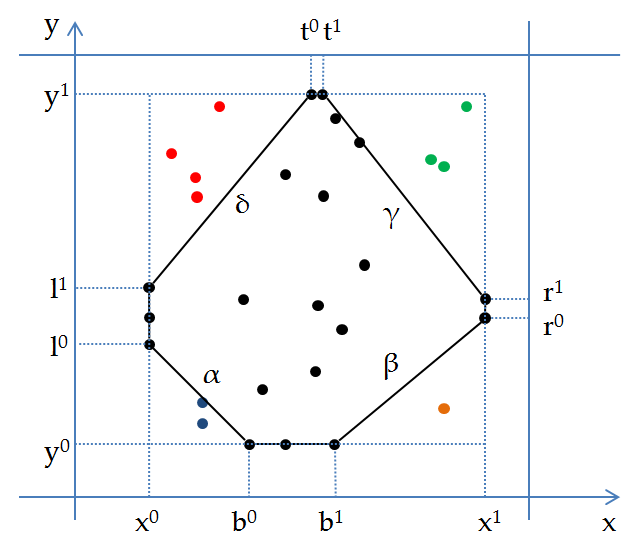
Дана последовательность точек на плоскости (для удобства её можно представлять двумя последовательностями координат точек: {x_i} и {y_i}). Пусть x⁰ = min_i x_i, y⁰ = min_i y_i, x¹ = max_i x_i, y¹ = max_i y_i, так что все (x_i, y_i) ∈ [x⁰, x¹]×[y⁰, y¹].

Теперь обозначим L = { y_i | x_i = x⁰ }, R = { y_i | x_i = x¹ }, B = { x_i | y_i = y⁰ }, T = { x_i | y_i = y¹ }. Обозначим l⁰ = min L, l¹ = max L, r⁰ = min R, r¹ = max R и т.д. Рассмотрим восьмиугольник (x⁰, l⁰)-(b⁰, y⁰)–(b¹, y⁰)-(x¹, r⁰)–(x¹, r¹)-(t¹, y¹)–(t⁰, y¹)-(x⁰, l¹).

Прямые α, β, γ и δ, проходящие через его стороны разбивают множество точек на пять групп:

Требуется написать программу, которая будет выделять четыре группы точек (все, кроме чёрных), записывая их в отдельные последовательности. Решение не должно содержать явных циклов.

Даны вектор точек и функция вычисления расстояния между двумя точками. Перебором (всех перестановок) найти такой порядок посещения всех точек, чтобы суммарная длина пути была минимальна. Решение должно содержать не более одного явного цикла.

Используя сортировку, перечислить все пары пересекающихся отрезков из заданного парой итераторов набора. Каждый отрезок задан парой значений (концов) типа, для которого определён компаратор, задающий строгий порядок (сравнение на <). Например, это могут быть числа (отрезки числовой прямой) или строки (диапазоны строк, словарный порядок).

Операция должна выполняться за O(N log N + K)-время и задействовать не более O(N) дополнительной памяти, где N — количество исходных отрезков, K — количество пар пересекающихся отрезков.

Пусть есть прямоугольный слой вещества, разбитый на кубы. Толщина слоя — один куб, а высота и ширина могут быть произвольными (целое число кубов). Каждый куб характеризуется одним числом в диапазоне [0, 1] — “коэффициентом поглощения”, т.е. долей поглощаемого излучения, проходящего через куб в любом из направлений вдоль любой из трёх координатных осей.

По матрице коэффициентов поглощения (слой) вычислить вектора совокупных коэффициентов поглощения по всем столбцам слоя и по всем строкам слоя.

Матрица задаётся диапазоном строк, строка — некий контейнер коэффициентов. Результаты записывать в последовательности, заданные итераторами, указывающими на начало. Решение не должно содержать явных циклов.

Так, при движении излучения вдоль второй строчки справа налево, получаем: 0.94375 = 1 – (1 – 0.9)(1 – 0.25)(1 – 0)(1 – 0.25).